Von unserem Mitglied

Dr. Richard Grimm
8.5.2009

zur pdf-Version hier klicken

Gegenstand dieser Arbeit sind grafische Darstellungen von Zeitreihen der statistischen Bundes- und Landesämter. Die Abbildungen befinden sich im Text, werden jedoch auch als selbstständige Excel-Dateien beigegeben. Die "Überlegungen zu Wirtschaftswachstum und Arbeitslosigkeit" werden fortgesetzt und vertieft.

Zusammenfassung:

1. Das vielzitierte Wirtschaftswachstum ist die Zunahme des Bruttoinlandsproduktes (BIP), die sich seit 1950 mit bemerkenswerter Stabilität vollzieht. Der zahlenmäßige Rückgang während einer Rezession war bisher, im Gegensatz zur Tiefe der öffentlichen Besorgnis, relativ gering.
2. Das preisbereinigte BIP wuchs linear, die Staatsschulden exponentiell. Obwohl wir einen regelmäßigen Kaufkraftzuwachs hatten, wuchs die Neuverschuldung proportional mit der bereits angesammelten Schuldenlast.
3. Das jährliche Wirtschaftswachstum ist eine Zufallszahl, die nicht vorherberechnet werden kann. Das Wachstum aller acht Rezessionsjahre bis 2003 (3 zweijährige, 2 einjährige Rezessionen) ist dadurch gekennzeichnet, dass der niedrige Zufallswert jeweils systematisch um weitere 10 Mrd €/a erniedrigt wurde.
4. Je größer die jährliche Zunahme der Arbeitslosigkeit, desto größer war die jährliche Neuverschuldung. Das heißt, die Arbeitslosigkeit wurde durch die Neuverschuldung finanziert, aber nicht bekämpft.
5. Es gibt mehrere Wechselwirkungen zwischen Bruttoinlandsprodukt und Arbeitslosigkeit. Sie entsprechen jedoch nicht dem einfachen Schema "großes Wachstum = weniger Arbeitslose, kein Wachstum = mehr Arbeitslose".

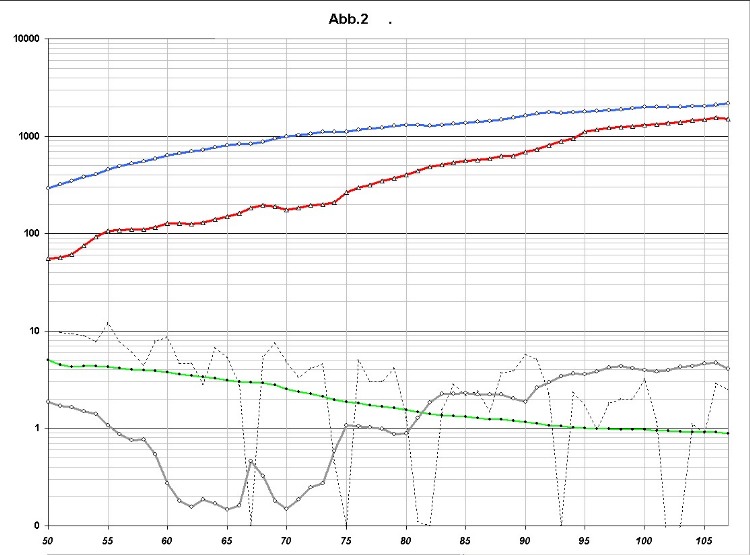
1. Volkswirtschaftliche Parameter (Abb. 1 und 2)

Die Abbildungen 1 und 2 zeigen, wie sich verschiedene volkswirtschaftliche Kennzahlen im Lauf der Jahre entwickelt haben. Die meisten Parameter sind zweimal dargestellt, nämlich einmal linear (Abb. 1) und einmal logarithmisch (Abb. 2). In linearer Darstellung bedeutet eine nach rechts ansteigende Gerade,

Abb. 1 Wirtschaftsparameter (linear)

Abb. 2 Wirtschaftsparameter (logarithmisch)

dass die durch sie dargestellte Kennzahl additiv nach dem Schema 0...1...2...3...4...5... mit der Zeit ansteigt.

Eine gleiche Gerade im logarithmischen System bedeutet einen multiplikativen Anstieg nach 1...2...4...8...16...32... .

Zur Erinnerung: Wenn man das Kapital K mit z. B. 5 Prozent pro Jahr (5% pa) x Jahre lang verzinst, wird die jeweils vorhandene Summe jedes Jahr erneut mit 1,05 multipliziert. Nach x Jahren ist das Anfangskapital K auf K(x) ("K von x") angewachsen nach der Formel

Die Zeit steht also im Exponenten, daher die Bezeichnung exponentielles Wachstum.

Die in den Abbildungen dargestellten Parameter sind:

a) Das Bruttoinlandsprodukt (BIP), blaue Kurve 1
Das BIP ist die Summe aller Güter und Dienstleistungen, die in einer Volkswirtschaft erzeugt wurden und die meistgebrauchte Kennzahl für deren Leistungsfähigkeit. Etwa drei Viertel davon ist das Volkseinkommen, nämlich die Summe der Löhne, Gehälter, Unternehmens- und Vermögenseinkommen. Der Rest besteht vor allem aus den Abschreibungen, sowie Produktions- und Importabgaben.

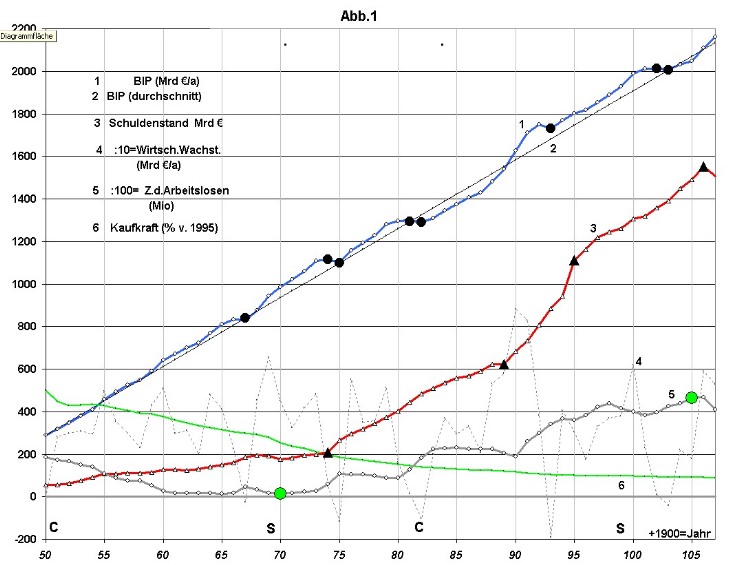
Die blauen Kurven 1 in den Abbildungen 1 und 2 zeigen die Entwicklung des BIP von 1950 bis 2006 aufgrund von Daten des Statistischen Bundesamtes (Destatis) in linearer bzw. exponentieller Darstellung. Es handelt sich hier um das deflationierte (auf ein konstantes Preisniveau bezogene) BIP. Es ist auf das Preisniveau von 1995 bezogen und wurde auf das Gebiet Gesamtdeutschland umgerechnet. Für die Gebiets-Umrechnung mussten die Zahlen von 1950 bis 1960 wegen der Eingliederung des Saarlandes und Westberlins mit dem Faktor 1.062 und danach von 1950 bis 1991 wegen der Wiedervereinigung mit dem Faktor 1,100 multipliziert werden. Die Faktoren entsprechen dem von Destatis jeweils angegebenen stufenweisen Anstieg des BIP in den Jahren der Eingliederungen.

In den Rezessionsjahren (schwarze Punkte der blauen Kurve in Abb. 1) würde man aufgrund der Tiefe der jeweiligen öffentlichen Besorgnis eigentlich einen spektakulären Absturz des BIP erwarten. Aber die bisherigen Rezessionspunkte markierten eher eine Rückkehr zu der Durchschnittslinie, die Anfang und Ende der BIP-Kurve geradlinig verbindet. Es wird zu diskutieren sein, ob der relativ moderate Rückgang des BIP wirklich als Ursache für das Ansteigen der Arbeitslosigkeit in diesen Jahren infrage kommt.

Da das BIP jährlich neu von null an gezählt wird, erreicht es am jeweiligen Jahresende eine Größe, die auf ein Jahr bezogen ist und daher in Mrd €/a (Milliarden Euro pro Jahr) angegeben wird. Es ist somit, ähnlich wie „km pro Stunde“, eine in „€ pro Jahr“ gemessene Geschwindigkeit.

Beim Auto erzeugt das Wirken der Geschwindigkeit (km/h) im Lauf der Zeit eine Zunahme der zurückgelegten Entfernung (km). Analog erzeugt die Geschwindigkeit BIP (Mrd €/a) im Lauf der Zeit das Anwachsen der seit 1950 aufsummierten Gesamtmenge aller jährlichen, in der Volkswirtschaft erzeugten Güter und Dienstleistungen (Mrd €). Während jedoch beim Auto die jeweils zurückgelegte Fahrstrecke der angestrebte Zweck des Systems ist, hat die jeweilige Gesamtmenge aller seit 1950 erzeugten Wirtschaftsgüter keine Bedeutung für unser tägliches Leben, weil der größte Teil davon sofort verbraucht wird. Uns interessiert das BIP selbst, denn es ist zu etwa drei Vierteln die Geschwindigkeit, mit der die Einkünfte aller Bürger (das "Volkseinkommen") auf die privaten Konten fließen.

Diese Geschwindigkeit ist jedoch nicht konstant. Jedes Jahr erzeugen wir im Durchschnitt mehr Wirtschaftsgüter als im Vorjahr. Deswegen verläuft die blaue BIP-Kurve 1 in der linearen Darstellung Abb. 1 nicht horizontal sondern ansteigend. Sie begann unter Adenauer im Jahr 1950 mit 290,6 Mrd €/a und stieg in den 55 Jahren bis 2005 auf 2072 Mrd €/a. Eine steigende Geschwindigkeit heißt Beschleunigung. Die Beschleunigung des BIP ist das viel zitierte und diskutierte „Wirtschaftswachstum“. Es hat die durchschnittliche Größe (Preise von 1995, Gesamtdeutschland)

Anmerkung: Eine Geschwindigkeit, z.B. "km/h", ist eine Längenänderung pro Zeiteinheit. Daher steht die Zeiteinheit linear im Nenner. Eine Beschleunigung ist dagegen eine Geschwindigkeitsänderung pro Zeiteinheit. Daher steht die Zeiteinheit quadratisch im Nenner. Beispiel: "Von null auf hundert in 3 Sekunden" bedeutet eine Geschwindigkeitszunahme um 100 km/h in 3 Sekunden = 100.000 m / 3600 sec / 3 sec = 100 000 m/( 3600 sec * 3 sec) = 9,26 m/sec^2 Diese Beschleunigung wäre fast so groß wie die des freien Falls mit 9,81 m/sec^2b)

Den durchschnittlichen Verlauf des BIP können wir durch eine Gerade symbolisieren, die bei 290,6 Mrd €/a beginnt, jedes Jahr um 32,39 Mrd €/a ansteigt und somit nach 55 Jahren 2072 Mrd €/a erreicht. Die im folgenden unter b) beschriebene Kurve 2 in Abb. 1 ist diese Gerade!

Ein physikalisches Modell für das BIP wäre eine Rakete im schwerelosen Raum, die, ausgehend von 290,6 km/h, durch eine gleichbleibende Schubkraft um 32,39 km/h^2 beschleunigt würde und nach 55 Stunden eine Geschwindigkeit von 2072 km/h erreicht hätte. Die während des beschleunigten Fluges zurückgelegte Entfernung entspräche der aufsummierten Gesamtmenge aller Wirtschaftsgüter.

b) Das durchschnittliche BIP-Wachstum (schwarze Gerade 2 in Abb. 1)
Diese Gerade beginnt im Jahr 1950 bei 299,6 Mrd €/a und verbindet die BIP-Werte von 1950 und 2006. Sie stellt den durchschnittlichen BIP-Verlauf grafisch dar und hat die Formel: BIP des Jahres x + 1950 =

Der Faktor von x ist die Steigung der BIP-Kurve und daher das Wirtschaftswachstum

Durch Integration dieser Geschwindigkeit BIP erhalten wir die Größe des Ergebnisses E dessen Wachstum die Geschwindigkeit "BIP" aufweist, also die Gesamtmenge aller seit 1950 erzeugten Wirtschaftsgüter in Mrd €. Die Integration der BIP-Gleichung ergibt

Bei Einsetzung von 55 für x (Jahre 1950 - 2005) berechnet sich E zu

Nach 55 Jahren sind somit etwa 75 % aller seit Beginn der Rechnung erzeugten Dienstleistungen und Güter nur durch das Wirtschaftswachstum entstanden. So wie für einen Menschen sein Lebenseinkommen nur eine hohe Zahl ohne unmittelbare Bedeutung ist, weil der größte Teil dieses Reichtums längst aufgezehrt ist, zeigt auch die Öffentlichkeit kaum Interesse für die Gesamtsumme aller BIP’s seit 1950.

Trotzdem ist die Größe E von Bedeutung als Maßzahl für alles was uns und kommenden Generationen von unserer wirtschaftlichen Betätigung bleibt.

Auf der positiven Seite stehen bei dieser Bilanz vor allem die Ergebnisse von Forschung, Technik und Erschließung die, wenn sie einmal zu mehr Wohlstand und Bequemlichkeit geführt haben, nicht mehr aufgegeben werden. Auf der negativen Seite steht der Verbrauch von Ressourcen wie Bodenschätze und Naturlandschaft sowie die Erzeugung langlebiger Abfälle wie CO2 und radioaktiver Müll.

Die Buchstaben C und S am unteren Rand der Abb.1 bezeichnen den Wechsel zu einer CDU- bzw. SPD-geführten Regierung. Eigentlich sollte man eine Art „Sägezahn-Kurve“ des BIP im Takt der Regierungswechsel erwarten. Denn nach einem solchen müsste die ehemalige Opposition ihre Wahlversprechen wahr gemacht und ein höheres Wirtschaftswachstum herbeigeführt haben, welches dann im Lauf der Regierungsjahre wieder abgesunken wäre usw. Es ist jedoch kein Einfluss eines Regierungswechsels auf# das Wirtschaftswachstum zu erkennen.

Nach jeder Wachstumsprognose der sog. Wirtschaftsweisen diskutieren die Medien intensiv über das mehr oder weniger große Ansteigen des BIP in dem betreffenden Jahr. Was jedoch kaum bemerkt oder kommentiert wird, ist die auffällige Richtungs-Konstanz der realen blauen BIP-Kurve, also die Beständigkeit unseres Wirtschaftswachstums über fünf Jahrzehnte hinweg. Immerhin hatten wir in den fünf Jahrzehnten seit Gründung der Bundesrepublik

• die Vollbeschäftigung mit Arbeitskräftemangel 1951 – 66
• den Anstieg der Arbeitslosenzahl ab 1974
• 5 Rezessionen ab 1967
• die unterschiedlich schnell steigende Staatsverschuldung
• mehrere Regierungswechsel
• die Wiedervereinigung

Die erstaunliche, über Jahre fortdauernde Unabhängigkeit von nationalen Ereignissen, deren Wirkung auf die Volkswirtschaft meist hoch eingeschätzt wird, führt zu der Hypothese:

Unser Bruttoinlandsprodukt wird durch Faktoren gesteuert, die nicht Bestandteil des deutschen Wirtschaftssystems sind. Die scheinbar so naheliegende Möglichkeit, das deutsche BIP selektiv zur steigern, dadurch die Arbeitslosen wieder zu beschäftigen und zugleich unseren Lebensstandard zu erhöhen, gibt es offenbar nicht (mehr).

Möglicherweise auch deswegen sind alle Versuche gescheitert, durch immer größere Neuverschuldung den Anstieg der Arbeitslosigkeit nachhaltig zu bekämpfen. Dies hätte nur durch eine ebenfalls nachhaltige Beschleunigung des Wirtschaftswachstums erreicht werden können, die in der blauen Kurve einen Knick nach oben bewirkt hätte.

An sich ist der globale Einfluss auf die nationalen Volkswirtschaften längst bekannt. Dabei stehen aber meist die zufälligen, relativ kurzfristigen Schwankungen, insbesondere die Weltwirtschaftskrisen, im Vordergrund des öffentlichen Interesses, nicht aber die langfristig stabilisierende Tendenz.

Die Einbindung der nationalen Volkswirtschaften in die Weltwirtschaft wäre vergleichbar einem Gespann aus vielen aneinander geschirrten Pferden, die gemeinsam eine Last ziehen. Selbst wenn eines der Pferde schneller ziehen könnte und wollte als die anderen, müsste es sich der Geschwindigkeit der Gruppe anpassen.

Die globale Wachstums-Stabilisierung verhindert Spitzen der BIP-Kurve nicht nur nach oben, sondern auch nach unten. Bei einer Schwäche des nationalen Marktes hilft oft der Export.

c) Das jährliche Wirtschaftswachstum (dünne, gestrichelte Kurven 4)
In der Durchschnittsgeraden 2 liegt jeder Jahrespunkt, so wie es die BIP-Formel ausdrückt, um 32,39 Mrd €/a höher als der des Vorjahres. In der Realität unterliegt das jährliche Wirtschaftswachstum jedoch Zufallsschwankungen nach oben und unten. In der Ökonometrie drückt man diese Zufallsabweichungen aus, indem man der BIP-Gleichung noch einen Summanden u ("weißes Rauschen") hinzufügt, der zufällige Abweichungen vom systematisch errechneten Kurvenverlauf beinhaltet.

In der linearen Darstellung (Abb. 1) wurde die absolute jährliche BIP-Zunahme in Mrd €/a^2 dargestellt, der Deutlichkeit wegen 10-fach überhöht. Der Durchschnittswert von 32,4 Mrd €/a^2 wäre eine Horizontale etwa in der Mitte zwischen den Linien 200 und 400. Das "weiße Rauschen" bewirkt, dass jeder Jahrespunkt durch Zufall so wie abgebildet nach oben oder unten verschoben wird. Diese regellose Verteilung der Punkte stützt die Vermutung, das jährliche Wirtschaftswachstum wäre eine Zufallszahl mit dem Durchschnitt 32,39.

In der logarithmischen Darstellung (Abb. 2) ist das relative (= prozentuale) Wirtschaftswachstum (Maßstab 1 : 1) dargestellt. Die Rezessionsjahre treten dadurch auffällig hervor, dass sie aus der Bandbreite der Zufallsschwankungen des BIP-Wachstums stark nach unter herausfallen. Anmerkung: Da negative Zahlen im logarithmischen System nicht darstellbar sind, wurden alle unter + 0,1 liegenden Werte (also auch negative) auf der Koordinate „0“, die der Zahl 0,1 entspricht, abgebildet.

In Prozenten gemessen betrug das Wirtschaftswachstum von jährlich gleichbleibend 32,4 Mrd €/a anfangs der 50-er Jahre fast 10 % des damaligen, relativ niedrigen BIP. Dagegen lag es 2005 wegen der mehrfach höheren Basis nur noch bei 1,5 %. Dementsprechend sinkt die Punkteschar der Kurve 3 von 1950 bis 2005 allmählich von der Linie 10 bis unter die Linie 2. Da das prozentuale BIP-Wachstum mit den Jahren kleiner wird, verläuft die BIP-Kurve 1 in Abb. 2 nicht geradlinig sondern abgeflacht.

Die volkstümliche Meinung: "Unter Adenauer und Erhard war das Wirtschaftswachstum viel größer!" gilt nur wenn man vom Wirtschaftswachstum allein die (relative) Prozentangabe kennt. Wäre diese tatsächlich seit den 50-er Jahren gleich hoch geblieben, dann müsste man die BIP-Kurve der ersten 5 Jahre in der logarithmischen Darstellung geradlinig verlängern und wäre im Jahr 2005 außerhalb der Grafik bei etwa 40.000 Mrd €/a angekommen.

Etwa 75 % des BIP sind das sog. Volkseinkommen. Bezogen auf die Zahl der Beschäftigten und preisbereinigt ist dieses seit Adenauers Zeiten etwa auf das 2,7-Fache gestiegen.

Dass heute trotzdem viele Menschen mit ihrer wirtschaftlichen Lage unzufriedener sind als damals, beruht nicht auf der Höhe des Volkseinkommens, sondern auf dessen Verteilung.

d) Die Arbeitslosenzahl (graue Kurve 5)
Die graue Kurve zeigt die Arbeitslosigkeit in den Originalzahlen (Bundesrepublik nicht auf Gesamtdeutschland hochgerechnet). Man kann den Verlauf in 4 Abschnitte gliedern:

1950 – 1962
Rückgang der Arbeitslosigkeit bis auf einen Minimalwert

1962 – 1966
Arbeitskräftemangel!

1967 – 1990
Starker Anstieg der Arbeitslosenzahl in den Rezessionen, dazwischen keine nachhaltige Abnahme. Lediglich nach der ersten Rezession 1967 wurde die entstandene Arbeitslosigkeit wieder vollständig abgebaut.

1990 – 2007
Nach der Wiedervereinigung starke Zunahme der Arbeitslosenzahl, zum Teil auch durch die Bevölkerungszunahme. Danach Stabilisierung auf hohem Niveau. Im Februar 2006 das Maximum von 5,0 Mio und Beginn eines erfreulich starken Rückgangs. Durch die gegenwärtige Rezession (2009) wird die Arbeitslosigkeit voraussichtlich abermals ansteigen.
   In der linearen Grafik könnte man den stufenförmigen Anstieg der Arbeitslosenzahl von 1970 bis 2005 näherungsweise durch eine Gerade ersetzen, welche diese beiden Punkte (grüne Kreise) verbindet. Diese hätte eine Steigung von ca. 0,15 Mio/a.

Ab 1970 lag das Wachstum der Arbeitslosigkeit, über die Rezessionen hinweg gemittelt, mehr als 30 Jahre lang bei 0,15 Millionen pro Jahr. Weder das zunehmende Bruttoninlandsprodukt noch die enorm steigende Verschuldung des Staates konnten dies verhindern.

e) Die Staatsverschuldung (rote Kurven 3)
Die roten Kurven 3 in der linearen und der logarithmischen Grafik stellen das Wachstum der Staatverschuldung dar (Preise 1995, Bund + Länder + Gemeinden; es ist entsprechend der BIP-Kurve auf Gesamtdeutschland hochgerechnet). Je größer die Steigung der Schuldenkurve, desto größer die jährliche Neuverschuldung. In der linearen Darstellung der roten Kurve von 1950 bis 2006 sind 4 Abschnitte unterschiedlicher Steigung zu unterscheiden, deren Grenzen durch vergrößerte schwarze Dreiecke markiert sind. Für jeden Abschnitt wurde die durchschnittliche Steigung, also die durchschnittliche jährliche Neuverschuldung, in Mrd €/a errechnet. Man vergleiche diese mit dem durchschnittlichen Wirtschaftswachstum von ca. 32 Mrd € pro Jahr. Die vier Abschnitte sind:

1950 - 1974 = 6,4 Mrd €/a
Das Problem Arbeitslosigkeit gab es damals nicht. Bei der ersten, noch harmlosen Rezession von 1967 reagierte man getreu nach Keynes mit einer mäßig erhöhten Neuverschuldung (kleiner Hügel der roten Kurve). Prompt ging die Arbeitslosigkeit zurück, und es geschah seit 1950 das erste und einzige Mal, dass Staatschulden abgebaut wurden, denn in den Jahren 1969/70 lief die rote Kurve ausnahmsweise abwärts.
   Man darf aber annehmen, dass die frühe und relativ geringe Arbeitslosigkeit auch ohne die Keynes-Aktion wieder verschwunden wäre.

1974 – 1989 = 27 Mrd €/a
Man wollte die unaufhaltsam steigende Arbeitslosigkeit durch steigende Neuverschuldung bekämpfen und nahm die Fruchtlosigkeit dieser Maßnahme nicht zur Kenntnis.

1989 – 1995 = 70 Mrd €/a
Offenbar griff man auch bei den Schwierigkeiten der wirtschaftlichen Wiedervereinigung nach dem Allheilmittel Neuverschuldung. Die logarithmische Darstellung zeigt, dass 1995 die rote Schuldenkurve der blauen BIP-Kurve bedenklich nahe gekommen war. Die Schuldenquote (das Zahlenverhältnis der Staatsschulden zum Bruttoinlandsprodukt) hatte 60 % überschritten, und die Bundesregierung sah sich zu Gegenmaßnahmen gezwungen.

1995 - 2006 = 51 Mrd €/a
Die Neuverschuldung ist immer noch untragbar hoch. Die Schuldenquote steigt weiter, wenn auch langsamer. Die in den letzten Jahren wiederholt angekündigte Absicht der Regierungen von Bund und Ländern, in einigen Jahren ohne Neuverschuldung auszukommen, ist wenig glaubwürdig.

In der logarithmischen Darstellung der Schuldenkurve (Abb. 2 , Kurve 3) fällt auf, dass sie nicht abflachend wie die BIP-Kurve, sondern im Prinzip geradlinig verläuft. Das bedeutet: Während unser nationales Einkommen linear wuchs, stiegen unsere Schulden exponentiell.

Je mehr Schulden wir bereits hatten, desto mehr neue kamen hinzu.

Man betrachte den langen Abschnitt von 1955 bis 1995 in der logarithmischen Darstellung. In dieser Zeit folgt die Kurve einer gedachten Geraden, welche in etwa die Zahlenwerte 100 und 1000 (Mrd €) verbindet. Die Schulden verzehnfachten sich demnach in diesen 40 Jahren. In derselben Zeitspanne stieg das BIP (vgl. Abb.1) von 460 auf 1800 Mrd/a, also auf das 3,9-fache.

Die Staatsschulden stiegen also mehr als zweieinhalb mal so schnell wie das BIP.

In der linearen Grafik Abb. 1 hat die rote Schuldenkurve im Jahr 1974 (dem ersten schwarzen Dreieck) einen deutlichen Knick nach oben. Vor diesem Knick entspricht die durchschnittliche Steigung der Kurve einer Zunahme der Schuldensumme um ca. 6,4 Mrd € pro Jahr (s.o.), von 1974 bis 2006 aber einer solchen von durchschnittlich 42 Mrd € pro Jahr. Wenn nun die durch Neuverschuldung bezahlten Investitionen des Staates — nach Keynes — Wirtschaftswachstum und Beschäftigung gesteigert, sowie die Arbeitslosenzahl gesenkt hätten, müsste ab 1974 die blaue BIP-Kurve stärker ansteigen als zuvor, und die graue Arbeitslosen-Kurve 5 dürfte sich zumindest nicht wesentlich über das Niveau von 1980 (knapp 1 Mio) erheben. Tatsächlich setzte sich aber die BIP-Kurve unverändert weiter in der Richtung der Durchschnittsgeraden fort und die Arbeitslosigkeit stieg in Wellen bis fast 5 Mio an.

Die exponentiell steigende Neuverschuldung bewirkte also weder ein stärkeres Wirtschaftswachstum noch verhinderte sie den Anstieg der Arbeitslosenzahl.

f) Die Kaufkraft der Währung (grüne Kurven 6)
In der Frühzeit der Bundesrepublik war die Kaufkraft der DM fast 5-mal so groß wie 1995. Die logarithmische Darstellung zeigt von 1950 bis 1969 einen mäßig starken Abfall der Kaufkraft-Kurve, der einer Inflationsrate von durchschnittlich 3,0 % pro Jahr entspricht. Mit dem Anstieg der Arbeitslosigkeit und der Neuverschuldung wird das Gefälle der Kurve bis 1995 im Durchschnitt mit 3,9 % etwas größer. Ab 1995 wurde neben den Maßnahmen zur Senkung der Neuverschuldung des Jahres 1995 auch die Geldentwertung gebremst.

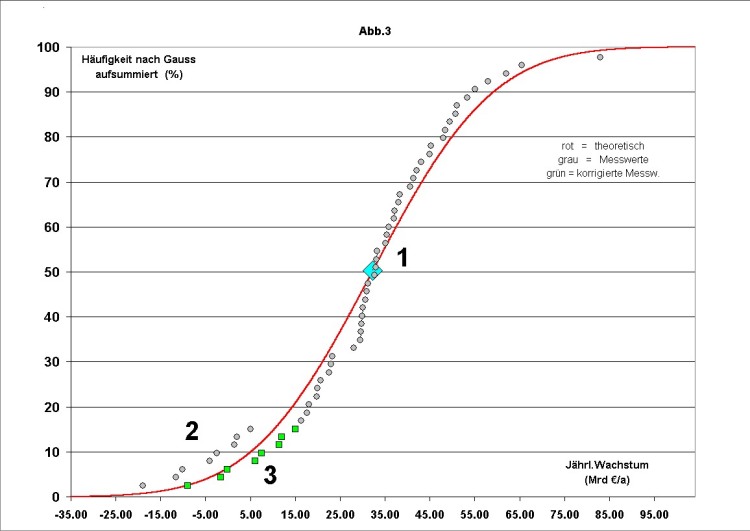
2. Die Gauß-Verteilung der Wachstumswerte (Abb. 3)

Das jährliche Bruttoinlandsprodukt wird von etwa 40 Millionen Beschäftigten in tausenden von Unternehmen aller Branchen in einer freien Marktwirtschaft erzeugt. Jede Arbeitsstunde, jeder Einkauf in den Geschäften, jede Nutzung eines Verkehrsmittels, jeder Vertragsabschluss usw. ist einer von sehr vielen Vorgängen, deren jeder irgendeinen Einfluss auf das am Jahresende erwirtschaftete BIP darstellt. Dessen jährliche Zunahmen sind also typische Zufallswerte, deren Durchschnitt gleich bleibt und deren Abweichungen vom Durchschnitt durch die Gauß’sche Wahrscheinlichkeitskurve wiedergegeben werden. Sie können nicht deterministisch vorausberechnet werden.

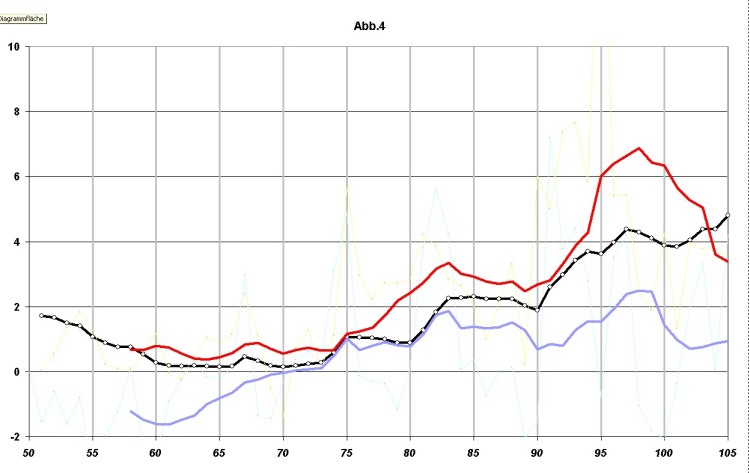
Abb. 3 Jährliches Wirtschaftswachstum auf integrierter Gauß-Kurve

Anmerkung: Die integrierte (S-förmige) Kurve wurde gewählt, weil die Zahl der Messwerte für eine Statistik nach der Grundform der Glockenkurve nicht ausreicht. Die Wahrscheinlichkeitssumme von 100 % wurde gleichmäßig auf alle vorhandenen Messwerte verteilt. Da sich die Gauß-Kurve jedoch von minus unendlich bis plus unendlich erstreckt, wurden vor der Verteilung die (relativ kleinen) Wahrscheinlichkeits-Werte bis zum ersten und ab dem letzten realen Messpunkt abgezogen. Die unterschiedliche Steigung der experimentellen Kurve ergibt sich nicht aus unterschiedlichen Wahrscheinlichkeiten je Messpunkt, sondern aus der mehr oder weniger dichten Besetzung mit Messpunkten, deren jeder den gleichen Anteil an Wahrscheinlichkeit in die wachsende Summe einbringt.

Die jährlichen Wachstumswerte sind — in der x-Richtung nach steigender Größe geordnet — als kleine graue Kreise eingezeichnet. Jeder Wert er-höht die Kurve um den gleichen Anteil an Wahrscheinlichkeit. Dort wo die Häufigkeit der Zufallswerte am größten ist — in der Nähe der Ziffer 1 — steigt die Kurve somit am steilsten an.

Die rote, S-förmig gebogene Kurve ist theoretisch nach der Gauß-Formel errechnet unter der Annahme, die Messwerte des absoluten Wirtschaftswachstums von 1950 bis 2005 seien allesamt echte Zufallsdaten. Das blaue Viereck markiert den Mittel- und Wendepunkt der theoretischen Kurve bei einer Wahrscheinlichkeitssumme von 50% und dem Mittelwert des Wirtschaftswachstums von 32,39 Mrd €/a. Dort liegen die Messwerte am dichtesten. Sie passen sich mit hinreichender Genauigkeit der Gauß-Kurve an.

Die Zahlenwerte des deutschen Wirtschaftswachstums sind somit Zufallsgrößen, die sich um einen Mittelwert (hier 32,39 Mrd €/a^2) gruppieren. Die Größe des Wirtschaftswachstums für ein bestimmtes Jahr kann im Voraus nur mit der nach Gauß berechneten Wahrscheinlichkeit angegeben werden. Eine exakte Vorausberechnung ist grundsätzlich ausgeschlossen.

Deswegen gehen die "Wirtschaftsweisen" (sollte man sie vielleicht mit "ai" schreiben??) bei ihrer jährlichen Wachstumsprognose von einer gedämpft optimistischen Variante des Vorjahres aus, beobachten das Wirtschaftsgeschehen und korrigieren den ersten Schätzwert in bestimmten Zeitabständen aufgrund der tatsächlichen Entwicklung mal nach oben, mal nach unten. Kurz vor Jahresende, wenn man dem Endwert schon sehr nahe ist, wird dann das endgültige Ergebnis verkündet.

Es ist jedoch nicht so, dass alle in Abb.3 eingezeichneten Messwerte sich in gleicher Weise in den Verlauf der roten Zufalls-Kurve einfügen. Eine kleine Gruppe von 8 besonders niedrigen Werten (die grauen Kreise bei der Zahl 2) liegt abseits der Gruppe 1. Sie liegen außerdem links von der roten Kurve, obwohl die untere Fortsetzung der Hauptgruppe 1 eher rechts davon zu erwarten gewesen wäre.

Diese 8 Punkte sind diejenigen der 8 Rezessionsjahre!

Zwischen den beiden Gruppen, also zwischen dem obersten Punkt der Gruppe 2 bei ca. +5 Mrd €/a und dem untersten Punkt der Gruppe 1 bei ca. + 15 Mrd €/a, liegen auffälliger Weise keine Messwerte, obwohl es innerhalb jeder Gruppe keine so große Lücke gibt. Würde man aber die Kreise der Achtergruppe um den Betrag dieser Lücke, also um etwa 10 Mrd €/a, nach rechts verschieben, so gelangten sie auf die durch grüne Quadrate markierten Stellen neben der Zahl 3. Durch diese Verschiebung würden sich die Rezessions-Werte dem Verlauf der berechneten Zufallskurve ebenso angleichen wie die normalen Zufallswerte.

Demnach sind die in jedem Jahrzehnt einmal auftretenden ein oder zwei Rezessionsjahre — und nur diese — dadurch gekennzeichnet, dass sie besonders niedrige Zufallswerte des Wirtschaftswachstums aufweisen, die außerdem systematisch um weitere 10 Mrd €/a nach unten verschoben sind. Es sind weiterhin die Jahre, in denen fast der gesamte Anstieg der Arbeitslosenzahlen stattfindet.

Eine Erklärung für diesen Befund könnte sein: Da die Produktivität je geleisteter Arbeitsstunde ständig wächst, aber das Bruttoinlandsprodukt nicht in entsprechender Weise mitwachsen kann, werden in der Volkswirtschaft ständig Arbeitskräfte entbehrlich.

Im letzten Jahrhundert galt die betriebsbedingte Entlassung von Mitarbeitern noch als Niederlage und nicht als gewinnsteigernde Maßnahme eines Unternehmers. Deswegen wurden die fälligen Entlassungen nicht sofort vorgenommen, sondern schubweise dann, wenn bei schlechtem Geschäftsgang — also bei besonders geringem Wirtschaftswachstum — eine beweisbare Notwendigkeit dazu bestand. Daher der plötzliche Anstieg der Arbeitslosen-Zahlen in den Rezessionsjahren.

Wäre wirklich das verringerte Wirtschaftswachstum in den Rezessionsjahren der Grund für den Anstieg der Arbeitslosigkeit gewesen, dann hätte diese nach Rückkehr der normalen Wachstumswerte wieder abnehmen müssen.

Die zusätzliche Erniedrigung des Wirtschaftswachstums in jedem Rezessionsjahr um 10 Mrd € gegenüber dem primären Zufallswert könnte man dem Wegfall der neuen Arbeitslosen als Konsumenten zuschreiben. Diese blieben aber meist auch in den Folgejahren arbeitslos, denn ab 1975 war der Rückgang der Arbeitslosigkeit nach jeder Rezession wesentlich kleiner als der vorherige Anstieg. Auch war die systematische Erniedrigung mit ca. 10 Mrd €/a stets gleich, während die Zahl der Entlassungen zwischen ca. 0,2 und 0,55 Mio pro Jahr schwankte.

Der Grund könnte, zumindest bei den Rezessionen 1967 bis 83 eine „Kaufzurückhaltung“ der (noch) Arbeithabenden gewesen sein, die zu einem Produktionsstau in der Konsumgüter-Industrie führte. In dieser Zeit lag die Zahl der Beschäftigten bei ca. 22 Mio. Verteilt man 10 Mrd € pro Jahr auf 22 Mio Beschäftigte, dann ergibt sich je Verdiener eine Ausgabenkürzung von ca. 38 € pro Monat. Von der Größe her erscheint diese Zahl glaubhaft. Nach der Rezession waren der beunruhigende Anstieg der Arbeitslosigkeit und die schlechten Wachstumsprognosen für die Davongekommenen erst einmal überstanden und das Angstsparen wurde wieder eingestellt.

Die etwa 9-jährige Periodizität der Rezessionen ist auf der Basis dieser Anschauungen so zu erklären, dass es einige Jahre dauert, bis sich durch den Anstieg der Arbeitsproduktivität ein gewisser Überhang an nicht mehr benötigten Arbeitskräften angesammelt hat. Erst dann konnte ein zufällig niedriges Wirtschaftswachstum zum Auslöser einer Rezession werden.

Demnach ist der irregulär starke Rückgang des Wirtschaftswachstums in den Rezessionsjahren eher die Folge als die Ursache der plötzlich zunehmenden Arbeitslosigkeit. Die primäre Ursache des langfristigen Anstiegs der Arbeitslosenzahlen ist die Steigerung der Arbeitsproduktivität.

Ab 1960 gab es mit gewisser Regelmäßigkeit in jedem Jahrzehnt eine Rezession. Die gegenwärtige Krise des Jahres 2009 bricht diese Regel, denn sie kommt früher und wird voraussichtlich schwerer als die vorangehenden. Ob sie aus der Gesamtheit der bisherigen Rezessionen herausfällt, kann derzeit noch nicht erkannt werden. Man muss stets bedenken, dass in unserer Welt jede Regelmäßigkeit durch zufällige Ereignisse außer Kraft gesetzt werden kann. Die Wahrscheinlichkeit eines zufälligen Ereignisses kann man jedoch nur abschätzen, wenn man über genügend viele beobachtete Zufälle der betreffenden Art verfügt.

Wenn man die Abb. 3 genauer betrachtet, gewinnt man den Eindruck, dass sich die Schar der Messwerte einer etwas steileren roten Kurve besser anpassen würden als der hier gezeichneten. Das trifft zu! Der Grund: Am linken unteren Ende der integrierten Gauß-Kurve sind bekanntlich 8 Messwerte systematisch nach links verschoben. Der letzte Messpunkt am oberen, rechten Ende der Kurve entstand 1991 nach der Wiedervereinigung. Sein Zahlenwert ist unwahrscheinlich hoch. Auch dieser Punkt ist offenbar systematisch beeinflusst. Bei der Konstruktion der roten Kurve war die systematische Verschiebung dieser 9 Messwerte nach außen noch nicht bekannt. Deswegen wurden alle Daten wie echte Zufallswerte behandelt und die rote Kurve geriet etwas zu breit. (Die errechnete Standard-Abweichung ist zu groß.)

3. Neuverschuldung und Arbeitslosigkeit (Abb .4)

In der folgenden Abb. 4 wird der langjährige Verlauf von Neuverschuldung und Veränderungen der Arbeitslosigkeit dargestellt. Es handelt sich dabei um zwei Geschwindigkeiten, nämlich diejenige in Mrd €/a, in welcher die Staatsverschuldung zunahm und diejenige in Mio/a, in welcher die Arbeitslosigkeit wuchs. Da die Zahlengrößen stark unterschiedlich sind, wurden die beiden Kurven in verschiedenem Maßstab dargestellt. Wegen der starken Streuung der Originalwerte (rote und blaue Punkte) wurde aus den Zickzack-Kurven mit Hilfe des Grafik-Systems der gleitende Durchschnitt von jeweils 9 Jahren gebildet, was in etwa dem Abstand der Rezessionen entspricht. So entstanden die rote Kurve der Neuverschuldung und die blaue Kurve der jährlichen Veränderung der Arbeitslosigkeit.

Bis 1971 sind die Werte der blauen Kurve negativ, wenn auch ansteigend. Das heißt, im Durchschnitt nahm die Arbeitslosigkeit ständig ab, wenn auch die Abnahme allmählich langsamer wurde. (Die relativ schwache Rezession von 1967 verschwindet im Durchschnitt). Die Neuverschuldung war im Durchschnitt kleiner als 10 Mrd € pro Jahr.

Abb. 4 Vergleich: Jährlicher Anstieg der Arbeitslosenzahlen / der jährlichen Neuverschuldung

Mitte der siebziger Jahre begann der bis heute andauernde Anstieg der Arbeitslosigkeit und der Staatsschulden (vgl. Abb. 1). Von da an zeigen die Kurven "Neuverschuldung" (rot) und "Veränderung der Arbeitslosenzahl" (blau) folgenden Verlauf:

1. Beide Kurven bewegen sich oberhalb der Null-Linie. Staatsverschuldung und Arbeitslosigkeit wachsen ständig. Anmerkung: Der zeitweise Rückgang der Arbeitslosigkeit zwischen den Rezessionen war so gering, dass er im Durchschnittswert verschwand.



2. Die beiden Kurvenverläufe sind ähnlich. Fast alle Richtungsänderungen von Arbeitslosenzahl und Staatsverschuldung nach unten und oben finden synchron statt.
   Das heißt: Je mehr neue Arbeitslose pro Jahr, desto höher die Neuverschuldung pro Jahr, und umgekehrt.



3. Der Abstand zwischen beiden Kurven bleibt aber nicht gleich, sondern er vergrößert sich im Lauf der Zeit. Das Verhältnis der Gipfelhöhen der roten zur blauen Kurve beträgt im Jahr 1983 etwa 1,8 und im Jahr 1998 etwa 2,7. Die Staatsverschuldung ist inflationsbereinigt (Preise 1995).
   Das heißt: Je höher die Arbeitslosenzahl im Lauf der Zeit anstieg, desto mehr Kredit pro Kopf der jährlich hinzukommenden Arbeitslosen wurde aufgenommen.

Die blaue Kurve stellt gewissermaßen die akute Veränderung der Krankheit „Arbeitslosigkeit“ dar und die rote die jeweils verabreichte Dosis des Gegenmittels „kreditfinanzierte staatliche Investition“. Das Ergebnis dieser Therapie war gleich null! Das beweist die schwarze Kurve in der Mitte, die den unaufhaltsamen Anstieg der Arbeitslosigkeit verdeutlicht.

Folgerung: Jahrzehntelang wurde durch die Neuverschuldung die Arbeits-losigkeit nicht bekämpft, sondern allenfalls finanziert. Bei der Aufnahme von Staatsschulden hat man sich an die Lehre von Keynes gehalten, die dazu gehörende Rückzahlung konnte jedoch nicht stattfinden, weil der Erfolg ausblieb.

Es ist kaum vorstellbar, dass 30 Jahre lang die Wirkungslosigkeit der kreditfinanzierten staatlichen Investitionen nicht erkannt wurde. Aber keine politische Partei wagt dem Volk zu sagen, dass wir auf absehbare Zeit mit der Arbeitslosigkeit leben müssen, und die Verwalter der öffentlichen Kassen haben sich zu sehr an die Einnahmen aus nicht zu tilgenden Krediten gewöhnt.

Der tiefere Grund für die steigende Arbeitslosigkeit in unserem Wirtschaftssystem ist die zunehmende Arbeitsproduktivität bei gleichzeitig global begrenztem nationalem Wirtschaftswachstum. Es werden jedes Jahr mehr Arbeitskräfte durch Automatisierung überflüssig als für das gleichmäßig steigende BIP gebraucht werden. Durch "deficit spending" kann der Staat die Entlassung nicht mehr benötigter Arbeitskräfte hinausschieben, aber nicht auf Dauer verhindern.

Die Behauptung, mit dem geliehenen Geld werde die Arbeitslosigkeit bekämpft, war eine Art doppelter "Lebenslüge": Damit wurden die vorschriftswidrig hohen Verschuldungen der öffentlichen Haushalte gerechtfertigt, und zugleich dem Volk Maßnahmen gegen die Arbeitslosigkeit vorgespielt.

4. Der Abbau der Staatsschulden

Der seriöse Zweck eines Kredites ist es, dem Verwender die Erarbeitung eines nachhaltigen, geldwerten Vorteils zu ermöglichen, aus dem er unter anderem auch Zins und Tilgung zahlen kann. Mit dem zurückgezahlten Geld kann die Bank andere Kredite vergeben und daraus Zinseinnahmen erzielen. Zur fortgesetzten Abdeckung von Haushalts- oder Bilanzdefiziten sind Kredite selbst dann nicht geeignet, wenn die Rückzahlung beliebig weit hinausgeschoben werden kann.

Das zeigt die folgende Tabelle. Für jedes der 5 Jahrzehnte wurden von den durchschnittlichen jährlichen „Einnahmen aus Krediten“ die Zinsausgaben (Annahme 5 % pa) für die bis dahin genommenen und nicht getilgten Kredite abgezogen und so eine Art durchschnittlicher, jährlicher „Nettogewinn“ errechnet.

Staatsschulden, Kredite und Zinsen
Jeweils Durchschnitt 19 Jahre, Preise 1995

Jahrzehnt, Beginn 19 . .		55	65	75	85	95
Schuldenstand	Mrd €	128	207	411	833	128
Kredite = Neuverschuldung pro Jahr	Mrd €/a	+4,2	+11,7	+29,1	+55,3	+35,9
5% Zinsen auf angesammelte Schulden	"	-6,4	-10,5	-20,5	-41,7	-64,5
"Nettogewinn" aus Krediten	"	-2,2	+1,2	+8,6	+13,6	-28,6

Man beachte, dass von 1965 bis 1994 immerhin ein positiver, hier so genannter "Nettogewinn" erzielt werden konnte. Mit dieser Einnahme konnten die Finanzminister und Kämmerer Investitionen bezahlen und indirekt die Verwaltungshaushalte aufbessern.

Nachdem aber 1995 die Neuverschuldung notgedrungen verringert wurde, verwandelte sich der "Nettogewinn" in ein Defizit von 28,6 Mrd €/a welches somit auch noch das durchschnittliche jährliche Wirtschaftswachstum von 33,4 Mrd €/a fast aufzehrte.

Die amerikanische Bankenkrise hat gezeigt, dass Banken nicht mehr weiterarbeiten können, wenn zahlreiche Kunden außerstande sind, ihre Kredite zurückzuzahlen. Es ist paradox, dass sich die Banken in ihrer heutigen Not ausgerechnet an den Schuldner wenden müssen, der seine Kredite grundsätzlich nicht zurückzahlt, den Staat. Und dieser Retter finanziert seine Hilfe mit noch mehr Schulden. Auf Dauer kann das nicht gut gehen!

Wer aber gibt einem solchen Schuldner sein Geld und gegen welche Sicherheit? Es sind diejenigen Bürger die Teile ihres Einkommens sparen können oder müssen, beispielsweise um eine private Alterssicherung aufzubauen. Ihr Vertrauen in den Schuldner Staat beruht auf dessen Möglichkeit, per Gesetz seine Steuereinnahmen von allen Bürgern einzutreiben, auch von denen, die wenig zum Sparen haben. Auf diese Weise sind die Zinsen für die Staatspapiere gesichert.

Das Kapital der Staatschulden kann jedoch aus Steuereinnahmen unmöglich zurückgezahlt werden. Falls eine Mehrheit der Gläubiger des Staates, auf den Gedanken käme, es in bar zu verlangen, dann würde keine Neuverschuldung mehr helfen und es käme lawinenartig zum Staatskonkurs. Die Bundeskanzlerin war also gut beraten, als sie den Bürgern die staatliche Sicherung für alle Spareinlagen versprach, denn nur durch Stillhalten aller Gläubiger kann die Finanzkatastrophe in Krisenzeiten verhindert werden. Das Thema Staatsschulden lassen die Politiker zurzeit ruhen.

Dagegen hielt noch im Mai 2007 der Bundesfinanzminister aufgrund günstiger Steuerschätzungen eine zeitlang "den Einstieg in den Abbau des aufgelaufenen Schuldenbergs von über 1500 Mrd Euro“ für möglich. "Wer Schulden aufnimmt, muss sie zuverlässig tilgen", sagte die Kanzlerin damals, "Neuverschuldung und Tilgung gehören zusammen" der Vizekanzler. Das Bundesland Hessen hoffte noch 2008 auf einen ausgeglichenen Haushalt für 2011. Im Haushaltsjahr 2009 sind jedoch Ausgaben geplant, die 112,9 Prozent der Einnahmen ausmachen. Die Hoffnung auf einen ausgeglichenen Haushalt richten sich jetzt "auf die Mitte des nächsten Jahrzehnts".

In allen Staaten mit Euro-Währung sollte — gewissermaßen als erster Schritt zum Schuldenabbau — die Neuverschuldung in auf 0,5 % des BIP gesenkt werden. Allerdings beeindruckt dieser gute Vorsatz etwa so wie die Versicherung eines Trinkers, seinen Konsum auf 0,5 Flaschen zu senken. Wer die glatte Null nicht schafft, scheitert auch an nullkommafünf! Der einzige Sinn hinter den Versprechungen der Politiker: Sie erinnern daran, dass unbegrenztes Schuldenmachen auch dem Staat eigentlich nicht erlaubt ist.

Alle gesetzlichen Vorschriften für Führung der öffentlichen Haushalte kennen für den Abbau von Schulden nur die ordentliche Tilgung. Da diese Selbstverständlichkeit aber nicht beachtet wird, konnte sie der Hessische Ministerpräsident Koch als interessanten Vorschlag in die Diskussion bringen. Sein Plan könnte beispielsweise folgendermaßen ablaufen:

Man tilgt

1500 Mrd € bei 5% Zinsen und 0,44% Tilgung in 50 Jahren

bis auf einen Rest von 200 Mio €. Es wäre eine gleichbleibende Zahlung (Annuität) von

erforderlich, in der bekanntlich der Anteil an Zinsen von Jahr zu Jahr kleiner und der an Tilgung entsprechend größer wird.

Für einen privaten Schuldner, der für eine einmalige Anschaffung einen großen Kredit aufnimmt und diesen anschließend in überschaubarer Zeit ver-tragsgemäß abzahlen will, ist die fällige Annunität ein wesentlicher und sorgfältig vorauskalkulierter Posten in seinen künftigen Budgets. Entsprechend wird man sich fragen, wie der Staat jedes Jahr fast 82 Mrd € für die Schuldentilgung aufbringen soll.

Aber der Staat ist kein ordentlicher Schuldner, sondern ein notorischer Schuldenmacher, und für einen solchen liegt das Problem anders: Seine größte Schwierigkeit ist der Verzicht auf die gewohnte Neuverschuldung!

Wäre dieser Verzicht erst einmal vom Vorsatz in die Tat umgesetzt, dann wären in unserem angenommenen Fall 92 % des Problems bereits gelöst. Denn die erste Annuität von 81,6 Mrd € bestünde vorwiegend aus den ca. 75 Mrd € an Zinsen, die stets im Haushalt veranschlagt sind, weil andernfalls die amtierende Bundesregierung die Zahlungsunfähigkeit Deutschlands erklären müsste.

Zusätzlich wäre dann nur noch der erste Anteil an Tilgung von 6,6 Mrd € aufzubringen. In Anbetracht der gegenwärtigen Finanzkrise (2008/09) sieht es allerdings so aus als würde Kochs Tilgungsvorschlag dieselbe Beachtung finden wie die gesetzlichen Vorschriften über die Deckung von Fehlbeträgen in öffentlichen Haushalten, nämlich keine.

Im Bundesfinanzministerium dagegen hält man die Vorstellung von einer ordnungsgemäßen Tilgung der Staatsschulden sogar der Öffentlichkeit gegenüber nicht mehr unbedingt aufrecht. "Wer weitere Milliardenpakete beschließt, gibt das Ziel der Konsolidierung der öffentlichen Haushalte auf" wurde Ende 2008 der Presse mitgeteilt. Dieser Denkrichtung entspricht der Plan, den der Minister selbst vor einiger Zeit verkündet hat: Die Schuldenquote (= Staats-schulden / BIP) soll von 60 auf 40 % gesenkt werden. Dies allerdings nicht durch Verringerung der Schulden im Zähler des Bruches, sondern durch eine zahlenmäßige Anhebung des BIP im Nenner. Aus diesem Grund soll das BIP nominal um 3,25 % pro Jahr steigen. Natürlich ist nicht an ein wirkliches Wachstum gedacht, denn die seit Jahrzehnten gewohnte reale Zunahme von 32,4 Mrd €/a^2 (Preise 1995) reicht nur für durchschnittlich 1,34 % pro Jahr (sofern sie auch weiterhin so groß bleibt). Der Rest von ca. 1,9 % pro Jahr soll aus Inflation bestehen.

Die Steinbrück'sche Schuldenquoten-Senkung könnte etwa so ablaufen, wie es die folgende Tabelle zeigt. Die Rechnung wurde von Jahr zu Jahr durchgeführt, angegeben wurden jedoch nur die Zahlen von Anfang, Mitte und Ende.

Anmerkungen zu Zeile:

1. Das langjährige Wirtschaftswachstum von 32,4 Mrd €/a (Preise 1995) in Preisen 2005 = 34,5 Mrd €/a. Dieses echte Wirtschaftswachstum würde durchschnittlich 1,34 % pro Jahr ausmachen.



2. Gesamt-Wachstum real + Inflation nach Steinbrück gleich 3,25 % pro Jahr; davon sind 3,25 – 1,34 = ca. 1,9 % auf Inflation zurückzuführen und bei der Verzinsung der Staatsanleihen zu berücksichtigen. Anmerkung: Der exakte Wert ist nicht die Differenz der Prozente, sondern der Quotient der Zinsfaktoren. 1,0325 : 1,0134 = 1,0188 = ca 1,019



3. Kaufkraft = BIP preisbereinigt : BIP jeweil. Preise. Wie nicht anders zu erwarten, führt die geplante Inflation zur Geldentwertung. Das ist von Bedeutung für alle privaten Altersversorgungen, beispielsweise für die Rücklagen von Unternehmen für Betriebsrenten ihrer Mitarbeiter.



4. Gleich 0,5% des BIP in jeweiligen Preisen nach der neuen EU-Regel. Aufgrund der momentanen außerordentlich hohen Neuverschuldung bestehen jedoch Zweifel, dass dieser niedrige Wert eingehalten werden können.

4 var: Deswegen wird alternativ eine ständige Verschuldung von 2% des BIP angenommen und als Variante var auch in den nächsten Zeilen der Tabelle angegeben

5. Durch Aufsummieren der jährlichen Neuverschuldung von 0,5% bzw. 2% des realen BIP ergeben sich die Schuldenhöhen 5 und 5 var.



6. Schuldenquote = Zeile 5 geteilt durch Zeile 2. Bei einer Neuverschuldung von jeweils 0,5% des BIP wird im Jahr 2027 tatsächlich das Steinbrück'sche Ziel von 40 % erreicht, bei höherer Verschuldung nicht.



7. 5% Zinsen + Inflations-Aufschlag 1,9 % = insgesamt 6,9 %

Ergebnis:

Die Steinbrück'sche geplante Inflation brächte in der Tat einen Rückgang der Schuldenquote von ca. 66 auf 40 % und damit auch einen geringeren Anteil der Schuldenzinsen am Steueraufkommen. Bleibt aber die Neuverschuldung auf Dauer nicht bei 0,5% des BIP, weil immer wieder Massenentlassungen und Störungen des gesamtwirtschaftlichen Gleichgewichts durch außerordentliche Neuverschuldungen abgewendet werden müssen, dann sinkt die Schuldenquote entsprechend langsamer, bis sie bei 2,0% Neuverschuldung praktisch konstant bleibt.

Von einer Sanierung der Staatsfinanzen kann bei diesem Plan keine Rede sein, denn

• die Kaufkraft der Währung sinkt auf jeden Fall,
• die Einhaltung von 0,5% des BIP als Neuverschuldung ist nach den praktischen Erfahrungen unwahrscheinlich,
• eine Tilgung von Staatsschulden ist nicht eingeplant.

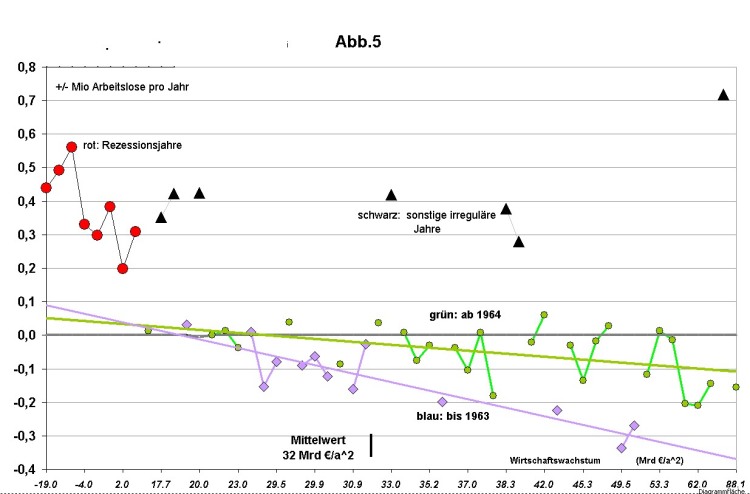
5. Die Abhängigkeit der Arbeitslosigkeit vom Wirtschaftswachstum (Abb.5)

In der Abb. 5 sind auf der x-Achse die Werte der jährlichen Veränderungen des BIP von - 19,0 bis + 88,1 Mrd € pro Jahr der Größe nach aufgereiht (nicht chronologisch). Die horizontalen Abstände sind nicht exakt maßstäblich, und die errechneten Ergebnisse sind wegen der starken Streuung der Messwerte nur als angenähert zu werten. Die Punkte im Diagramm sind die im Lauf der Jahrzehnte gemessenen, zum jeweiligen Wachstumswert gehörenden Veränderungen der Arbeitslosigkeit.

Nach der landläufigen Vorstellung von der Wirkung des Wirtschaftswachstums auf die Arbeitslosigkeit müsste dieses Diagramm eigentlich aus einer einzigen Linie oder Punkteschar bestehen, die sich von links oben nach rechts unten erstreckt und im mittleren Bereich die Null-Linie unterschreitet. Das hieße: Bei negativem oder sehr geringem Wirtschaftswachstum deutliche Zunahme der Arbeitslosigkeit, bei hohem Wachstum deutliche Abnahme und bei mittlerem Wachstum keine wesentliche Änderung.

Abb. 5 Jährliches Wirtschaftswachstum und Veränderung der Arbeitslosigkeit

Wenn man sich die farbig unterschiedenen Messpunkte gleich aussehend vorstellt, würde das Diagramm dieser Erwartung keineswegs entsprechen, sondern widersprüchliche Aussagen liefern. Die obere (rote und schwarze) Punkteschar über die gesamte Breite des Diagramms würde besagen: Deutliche Zunahme der Arbeitslosigkeit kann bei hohem und niedrigem Wirtschaftswachstum eintreten.

Die untere (grüne und blaue) Punkteschar auf und unter der Null-Linie dagegen: Bei geringem Wirtschaftswachstum gleichbleibende Arbeitslosigkeit, bei hohem Wirtschaftswachstum teils gleichbleibende, teils abnehmende Arbeitslosigkeit.

Aus diesem Befund ist zu schließen, dass es nicht eine, sondern mehrere Beziehungen zwischen Wirtschaftswachstum und Arbeitslosigkeit geben muss. In der Tat konnten die Messdaten in 4 solche Abhängigkeiten aufgeteilt und farbig unterschieden werden.

a) Blaue Rhomben
Diese Werte zeigen die Veränderung der Arbeitslosigkeit in Abhängigkeit vom jährlichen Wirtschaftswachstum (Mrd €/a^2) für die Jahre 1950 bis 1963, also für die Zeit des „Deutschen Wirtschaftswunders“. Die blaue Gerade ist die vom Grafik-System gezeichnete lineare Trendlinie, die aus den stark streuenden Messwerten einen durchschnittlichen Verlauf konstruiert. Je steiler eine solche Linie abfällt, desto mehr Arbeitsplätze schafft ein Ansteigen des Bruttoinlandsproduktes.

Bei einen Wirtschaftswachstum von ca. 19 Mrd €/a^2 schneidet die blaue Trendlinie die Null-Linie. Das war damals also die „Arbeitsplatz-neutrale“ jährliche BIP-Zunahme, bei welcher die Arbeitslosigkeit prinzipiell unverändert blieb. Sie liegt ca. 13 Mrd. unter dem Mittelwert des Wirtschaftswachstums von ca. 32 Mrd. Links von diesem Wert befinden sich keine blauen Punkte. Demnach nahm die Arbeitslosigkeit damals fast immer mehr oder weniger rasch ab, aber niemals zu.

Bei etwa 50 Mrd €/a^2 erreicht die blaue Trendlinie den Wert - 0,3 Mio. 50 Mrd liegen etwa 30 Mrd rechts vom Schnittpunkt mit der Null-Linie. Eine jährliche BIP-Steigerung um 30 Mrd €/a brachte damals eine Abnahme der Arbeitslosenzahl um 0,3 Mio pro Jahr. Das heißt, ungefähr zusätzliche 10 Mrd € pro Jahr an BIP erzeugten zusätzliche 0,1 Mio Arbeitsplätze. Das wären für einen neu entstehenden Arbeitsplatz rechnerisch 100 000 €.

Der durchschnittliche Arbeitgeber stellte demnach eine Arbeitskraft ein, wenn er die Aussicht hatte, mit ihrer Hilfe seinen Umsatz in etwa um 100 000 €/a zu steigern.

Anmerkung: Genau genommen ist darunter der Umsatz mit einem Endprodukt zu verstehen, welches alle Mehrwerte der Vorprodukte mit einschließt.

b) Grüne Kreise

Die grünen Punkte zeigen die Veränderungen der Arbeitslosenzahl ab 1964. Nach dem Rückgang der Arbeitslosigkeit auf das Minimum von 1962 und 5 Jahre vor der ersten, noch harmlosen Rezession war die Arbeitswelt eine andere geworden. Statt sinkender hatten wir fortan beträchtlich steigende Arbeitslosigkeit.

Allerdings kann dies nicht an der grünen Trendlinie gelegen haben, denn diese zeigt selbst bei Nullwachstum des BIP so gut wie keine Zunahme der Arbeitslosigkeit an. Andererseits schneidet sie die Null-Linie bei einem Wirtschaftswachstum von ca. 28 Mrd €/a^2, das heißt, erst ab diesem Wert, der fast den Mittelwert von ca. 32 Mrd erreicht, schaffte das Wirtschaftswachstum damals Arbeitsplätze. Die Trendlinie verläuft wesentlich flacher als in der Periode 1950 bis 1963 und sinkt je + 30 Mrd €/a nur um ca. 0,1 Mio Arbeitslose pro Jahr. Die Unternehmen stellten damals (rechnerisch-schematisch) nur noch ein, wenn sie von einem neuen Mitarbeiter einen Mehrumsatz etwa in der Größenordnung von 300 000 € pro Jahr erwarten konnten.

Die grünen und die blauen Punkte verhalten sich trotz der starken Streuung in etwa so, wie man sich die Abhängigkeit der Arbeitslosenzahlen vom Wirtschaftswachstum vorstellt. Diese Messwerte können als reguläre Werte bezeichnet werden.

Es sind jedoch nicht alle Messwerte ab 1964 in der grünen Punkteschar enthalten, denn die in den folgenden Abschnitten beschriebenen liegen unverkennbar weitab von dieser.

c) Große rote Kreise
Diese Punkte gehören zu den 8 Rezessionsjahren. Sie bringen die systematische Erniedrigung des Wirtschaftswachstums um 10 Mrd €/a^2 und die besonders große Steigerung der Arbeitslosigkeit zum Ausdruck. Um auf die Höhe der roten Punkte zu kommen, müsste man die grüne Trendlinie vom Schnittpunkt mit der Null-Linie bei ca. 30 Mrd €/a nach links bis etwa minus 170 Mrd €/a^2 verlängern. Man sollte also den Zusammenhang zwischen Wirtschaftswachstum und Arbeitslosigkeit in diesen Jahren als irregulär bezeichnen.

Die Unternehmen haben in den Rezessionsjahren wesentlich mehr Arbeitskräfte entlassen, als dem Rückgang des BIP-Zuwachses entsprochen hätte. Das geringe Wirtschaftswachstum kann zwar der Anlass aber nicht der Grund für die Entlassungen gewesen sein.

d) Schwarze Dreiecke (Abb. 5)
Diese irregulären Werte markieren starke Zunahmen der Arbeitslosigkeit außerhalb der eigentlichen Rezessionsjahre in der Größenordnung 0,3 bis 0,4 Mio pro Jahr, und das sogar bei gutem Wirtschaftswachstum, in welchem die Arbeitslosigkeit ansonsten deutlich abnimmt. Drei dieser Punkte folgten auf die drei Rezession ab 1981/82, und die übrigen 4 betreffen die Zeit nach der Wiedervereinigung. Die letzteren dürften von Vereinigungsbedingten Sonderentwicklungen verursacht worden sein.

Auf der Basis der Abb. 5 kann man folgende Bilanz der Arbeitslosenzahl von 1951 bis 2005 aufmachen:

Langfristige Bilanz der Arbeitslosigkeit

Anmerkungen (1) – (3)